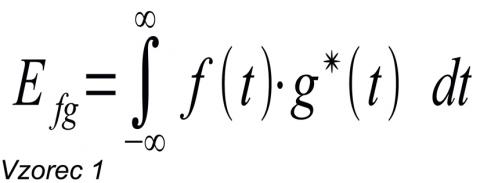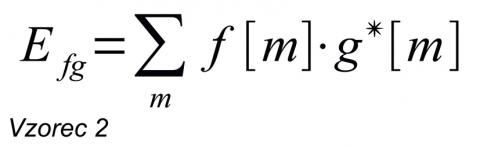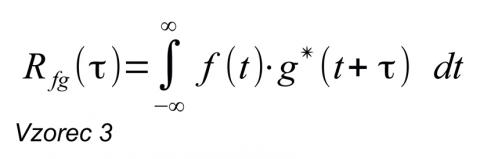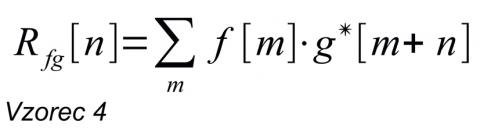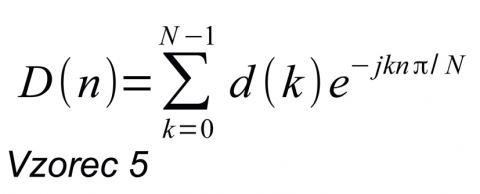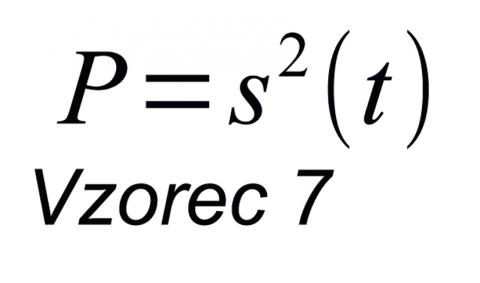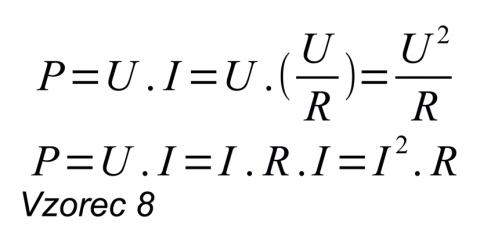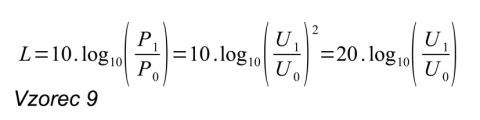Myslím si, že je dobré vědět, čím a proč točím a čeho chci dosáhnout. Navíc jsem přesvědčen, že znalosti (alespoň rámcově) obsažené v tomto článku by měly již z hlediska stavovské cti patřit k technickému základu každého opravdového zvukaře, nebo alespoň toho, kdo zároveň vykonává práci v zahraničí zvanou system engineer. Reakce typu „k čemu to je“ a „v praxi je to přeci úplně jinak“ s radostí přenecháme méně náročným kolegům.
Ještě pro pořádek – v článku se objeví pár základních vzorečků, nicméně je uvedu jen pro úplnost (nebo pro další studium), většinou nebude třeba provádět žádné výpočty. Podstatné je pochopit myšlenku, která za tím stojí a je jedno, zda ze vzorečku, z komentáře, nebo z obou. Nenechte se jimi tedy odradit a klidně je přeskočte. Já sám vzorečky při čtení také přeskakuji, a obvykle se k nim vracím až při třetím nebo dalším čtení. A ještě jedno doporučení – pochopení některých složitějších jevů vyžaduje určité duševní úsilí. Nebojte se na chvíli zapojit mozek, abyste danou věc pochopili. Je to lepší, než donekonečna čekat, zda přijde nějaké jiné zázračné vysvětlení, které bude hned jasné. Ono taky nemusí přijít prostě proto, že daná věc není úplně jednoduchá...
A začneme zostra
Byť se to možná bude zdát nezvyklé, osobně pokládám za základní nástroj/princip pro pochopení dále diskutovaných postupů pojmy Vzájemná energie a Korelace. Nenechte se zaskočit, dál už to bude brnkačka. Klasická moudrost však praví: „Než můžeme začít něco dělat, je obvykle potřeba udělat před tím ještě něco jiného“. Ani zde nebudeme výjimkou – v rychlosti ještě prolétneme základní klasifikaci signálů:
• Energetické signály – jsou neopakující se signály, jejichž celková energie je konečná. Mají proto spojité spektrum.
• Výkonové signály – jsou typicky šumové nebo periodické signály, jejichž maximální výkon je konečný, avšak celková energie závisí na délce trvání/měření. Proto se charakterizují výkonem, střední hodnotou (průměrná hodnota) atd.
• Periodické signály – patří mezi výkonové signály a vyznačují se tím, že lze nalézt určitý minimální časový interval, o který když funkci posuneme, bude vypadat zcela stejně – funkční hodnoty funkce se tedy po nějakém čase budou opakovat. Spektrum periodických signálů je čárové, protože může být tvořeno pouze a jedině složkami, které jsou celistvým násobkem periody (jinak by nešlo o periodické signály).
• Diskrétní signál – v čase nebo v amplitudě znamená, že v daném rozměru nabývá signál jen určitých hodnot, je nespojitý (typicky vzorkovaný v čase)
• Digitální signál – je diskrétní v čase i amplitudě (je vzorkován a kvantován)
• Vzorkovaný signál – má automaticky periodické spektrum – za předpokladu teoreticky ideálně krátké doby sejmutí vzorku totiž nevíme, co se dělo v době mezi odebráním vzorků – teoreticky tak mohlo proběhnout libovolně mnoho period signálu; praktickým projevem tohoto faktu je aliasing (vzorkuji-li sinus 15 kHz s frekvencí 20 kHz, bude výsledné spektrum obsahovat v pásmu 0 – Fs složky 5 kHz a 15 kHz)
Vzájemná energie
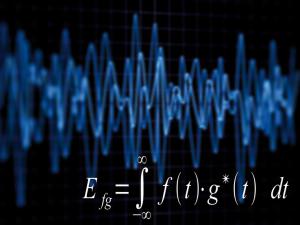
Jde o zásadní pojem, vyjadřující de facto souvislost mezi signály. Typickým příkladem je situace, kdy je signál tvořen více složkami (superpozice více elementárních signálů, například sinus o rů-zných frekvencích). Výpočtem vzájemné energie pak lze zjistit, jak velkou část energie tvoří ta která složka, takže v důsledku můžeme signál za určitých podmínek rozebrat na jednotlivé složky:
Jde o integrál dvou funkcí přes celý interval (od minus nekonečna do nekonečna, nebo alespoň tam, kdy jsou obě funkce nenulové). Matematicky to neznamená nic jiného, než že všechny body funkce (vždy po jednom z každé v daném okamžiku) spolu vynásobíme a výsledek sečteme. Protože programy pracují s digitálními signály, bude možná ještě jasnější přepis pro diskrétní funkce (kde integrál nahradí ekvivalentní operace – sumace):
Možná vás ta trocha matematiky vyděsila, ale nebojte se, jsou to jen kupecké počty. Jde o vzorce pro vzájemnou energii signálů f(t) a g(t) ve spojitém a v diskrétním čase (vzorkované nebo zdigitalizované signály). Hvězdička značí komplexně sdruženou funkci, tedy obrácení znaménka imaginární části v případě komplexní funkce, neboť vzájemná energie je ve výsledku reálná... zkrátka ji pro naše „myšlenkové“ účely můžete v takzvaném prvním přiblížení ignorovat. Dále než do prvního přiblížení se zde pouštět stejně nebudeme.
Ale zpět k jádru věci. Máme-li dva signály, které spolu vůbec nesouvisejí, bude při vzájemném „překrytí“ jejich průběhů prakticky shodná část, kdy se překrývají, s částí, kdy se míjejí (například překryv 1 kHz a 2 kHz sinus). Když tedy sečteme překryvy (kde mají obě funkce shodnou polaritu v daný okamžik) a odečteme „míjení“ (rozdílné polarity v daném okamžiku), dostaneme více méně nulu. Když spolu ale signály nějak souvisí, výsledkem již nebude nula. Zde není důležitý vzájemný poměr velikostí obou signálů/funkcí, který udává jen měřítko, ale plocha překryvu.
Korelace
Toto prapodivné slovo v našem případě označuje konkrétní případ integrální transformace, kterým lze spočítat vzájemnou souvislost či souvztažnost dvou signálů, a na kterém je hlavní myšlenka dobře patrná. Zní to možná kostrbatě, ale snad to bude jasnější ze vzorečku:
Dobrá, možná to tak jasné není, ale neházejme flintu do žita. Máme dvě funkce f(t) a g(t). Levá strana vzorce představuje pouze zápis „korela-ce funkcí f(t) a g(t) v závislosti na jejich vzájemném posunutí o t“ v podobě, používané v teorii signálů. Pozornější si možná všimli, že jde téměř o vzorec pro vzájemnou energii, pouze se ze členu na levé straně stala funkce (vzájemná energie je jen číslo, tedy tzv. skalár) a na pravé straně přibyl jedné funkci v argumentu parametr. Výpočet vzájemné energie dvou funkcí, což je jedna hodnota, tak přešel ve funkci závislosti vzájemné energie dvou funkcí na jejich vzájemném posunutí, což nazýváme korelační funkcí. Je totiž celkem jasné, že plocha překryvu a tedy vzájemná energie se bude měnit podle posunutí. V diskrétním čase bude výpočet vypadat následovně:
Tady je to už myslím jasné (doufám). Uvažujme nejprve nulové vzájemné posunutí signálů (n = 0) – v rámci množiny bodů m (tedy m vzorků signálu) provedeme v každém kroku násobení vzorku f(0) a g(0), ve druhém kroku f(1) a g(1) a tak dále. Výsledky jednotlivých násobení sečteme. Výsledkem pak bude korelace signálu f[m] a g[m] při nulovém vzájemném posunutí a de facto obdržíme stejnou hodnotu, jako při výpočtu vzájemné energie. Pro jiné posunutí, kdy bude n jiné než nula, samozřejmě bude korelace jiná (asi tak jako překryv dvou funkcí sinus 1 kHz, posunutých navzájem např. o 90° nebo 180°).
Jak vidíte, vlastně nejde o nic jiného, než opravdu o kupecké počty – sčítání a násobení. Není samozřejmě potřeba nyní nic násobit, postačí si jen představit, že je možné tímto způsobem například zjistit, jakou měrou je v neznámém signálu (a zda vůbec) obsažena složka sinus 1 kHz. Výsledkem jedné operace integrování/sumace přes celý interval je jedna hodnota – korelace obou funkcí pro jejich vzájemné posunutí o n.
Nyní se to možná zdá jako zbytečná matematická exhibice, ale schopnost si alespoň představit, jakým způsobem se podobné věci provádějí, je zásadní pro pochopení principu dalších operací se signálem, kterých se při nastavování aparátu provádí celá řada, a pro získání citu pro věc. Alespoň zevrubné povědomí o těchto operacích rovněž postačí k tomu, abyste si udělali lepší představu o tom, co může a nebo nemůže být možné spočítat, jak ovlivní jednotlivé parametry přesnost výpočtu spektra atd. Zdá se vám to složité? Tak si představte, že tato matematika pochází z doby Isaaca Newtona, i když integrální transformace jsou jen přes 200 let staré. Když by tehdy chtě- li lidé vypočítat nějakou takovou funkci numericky jen v pár bodech, trvalo by jim to několik hodin, snad i dnů. Dnes stačí napsat pár vzorců do tabulkového procesoru a je hotovo...
Impulzní odezva a frekvenční charakteristika
Čistě pro pořádek jen uvedu, že následující operace se týkají lineárních systémů, tedy těch, kdy stejné změně amplitudy vstupního signálu odpovídá stejná změna výstupního signálu. U limitujícího zesilovače, reproduktoru mimo lineární oblast atd. to tedy neplatí. (Ilustrace 1)
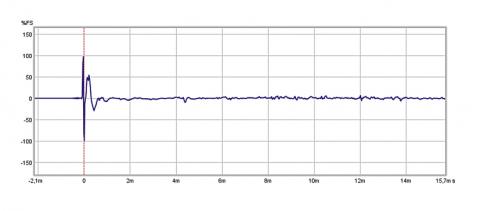
Tedy impulzní odezva je odezva systému na impulz. Jinými slovy: do vstupu systému (zkoumaného zařízení) pošlu impulz (puristé dokon-ce diracův, nám postačí uvažovat jeden vzorek s maximální amplitudou, všechny ostatní nulové) a zkoumám výstupní signál. Pokud mám štěs- tí a v reálném světě se mi odezva neztratí v šumu, dostanu na výstupu to, čemu se říká impulzní odezva. Ta je velmi užitečná zejména proto, že v ní je obsažena kompletní informace o frekvenční charakteristice zkoumaného systému.
Onen diracův impulz (nebo nejkratší reálně vyrobitelný impulz, který se vzhledem ke zkoumanému systému chová stejně, jako diracův) má totiž tu vlastnost, že jeho amplitudové spektrum je jednotkové a fázová charakteristika je nulová. Jinými slovy obsahuje všechny frekvence se stejnou úrovní, které mají navíc shodnou fázi (začínají ve stejný okamžik). Pokud takovýto signál pošlu přes zkoumaný systém, výstup bude (lineárně) zkreslen jeho frekvenční charakteristikou. Spočítám-li tedy spektrum impulzní odezvy systému, budu znát kompletní frekvenční charakteristiku (v komplexní podobě, tedy i s fází)! Docela užitečné, nemyslíte? Navíc to není nic nepředstavitelného. Ideální (diracův) impulz představuje modelový energetický signál s ideálně plochou frekvenční charakteristikou (modulovou i fázovou), až na tu fázi je tedy podobný bílému šumu (což je ale výkonový signál), který se také někdy používá pro měření frekvenční charakteristiky, dokonce častěji, než skutečné impulzy.
Jak se jen ta frekvenční charakteristika počítá?
Řada programů pracuje takovým způsobem, že nějakou cestou získá impulzní odezvu, v naprosté většině nepřímo. Jakmile je tato odezva spočítána, provede se výpočet spektra této odezvy, neboť jak již víme, impulzní odezva je v podstatě jakýmsi obrazem frekvenční nebo chcete-li přenosové charakteristiky.
Za způsob výpočtu spektra v podstatě vděčíme francouzskému matematikovi z období první francouzské revoluce Josephu Fourierovi. Ten jako první přišel na způsob složení signálu z jednotlivých elementárních (správně bázových) funkcí (tzv. Fourierových řad). Zní to možná složitě, ale v podstatě se mu podařilo matematickou funkci (resp. signál) složit (přesněji aproximovat) z řady tzv. bázových funkcí. Co na tom, že tyto postupy používal k řešení rovnic vyjadřujících vedení tepla. Dnes z pohledu zvuku bychom řekli, že dokázal jako první skládat funkce ze spektrálních složek, a tak de facto definoval i spektrum, i když to nemusel mít v úmyslu. Z filozofického hlediska nel-ze říci, že signál by se doslova skládal ze spektrál- ních složek – takový zvuk existoval dávno předtím, než lidstvo vynalezlo matematiku a spektrum. Přesnější je říci, že se znalostí časového průběhu dokážeme určitým způsobem vytvořit řadu dílčích elementárních funkcí, ze kterých poté složíme signál, jež bude mít v porovnání s původním signálem minimální rozdílovou energii, takže bude informačně prakticky totožný. No a sadu koeficientů, které charakterizují konkrétní konfiguraci elementárních funkcí pro daný signál, nazýváme spektrum signálu.
Diskrétní Fourierova transformace (DFT)
Jen pro pořádek uvedu vztah pro výpočet DFT
kde n je index bodu spektra, k je index vzorků časového signálu a N je počet vzorků. Aby úrovně v amplitudovém spektru lépe odpovídaly úrovním signálu, násobí se výsledek hodnotou 1/N, jinak tato operace probíhá až při výpočtu časového průběhu ze spektra, tzv. inverzní DFT. Aby bylo jasné, že nejde jen o planou exhibici, ale sku- tečně takto lze něco vypočítat, uvádím ještě kousek kódu z makra souboru Harmonická syntéza.ods (viz dále), které počítá DFT, a kterým bylo spočítáno spektrum v ilustraci číslo 3.
Na první pohled to tak sice nevypadá, ale jde skutečně o zápis DFT. Protože ale řada programovacích jazyků nezvládá počítat v komplexním oboru (viz dále), je výpočet rozdělen na reálnou a imaginární část za použití věty rozkladu komplexní exponenciály:
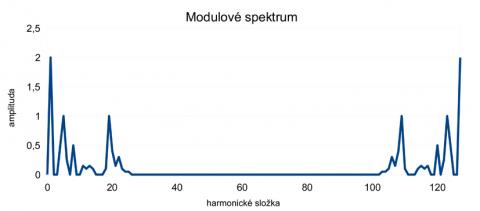
Z reálné a imaginární složky je pak za použití Pythagorovy věty a související goniometrie vypočten úhel fázoru podle poměru reálné a imaginární složky (viz dále). Na následujících obrázcích jsou uvedeny příklady časového průběhu délky 127 vzorků a odpovídajícího spektra. (Ilustrace 2 a 3)
Nejjednodušeji lze lidsky výpočet koeficientů spektrálních složek (= bodů frekvenční charakteristiky) popsat jako proces obdobný zjišťování vzájemné energie každé složky se zkoumaným signálem. Když pak jednotlivé koeficienty vyneseme do grafu, jehož osami budou frekvence a úroveň (amplituda), získáme tak v podstatě spektrum daného signálu.
Kdybychom pak provedli inverzní transformaci, tedy poskládali signál pomocí všech spektrálních složek, bude se rozdíl energie původního a aproximovaného signálu limitně blíží nule. No a protože nositelem informace je vždy energie, lze úvahu posunout dále tím způsobem, že aproximovaný signál bude nést prakticky stejnou informaci, jako původní, a bude tedy svým spektrem v ideálním případě plně definován.
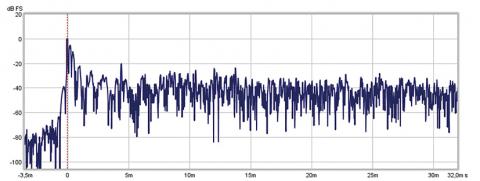
ETC
Enery-Time Curve je jen způsob zobrazení impulzní odezvy v logaritmické škále, která lépe odpovídá vnímání sluchem. Protože nelze logaritmovat záporná čísla a logaritmická škála slouží k porovnání energetických/výkonových poměrů signálů, je potřeba před logaritmováním převést signál na vyjádření jeho výkonu. To provedeme jednoduše:
kde s(t) je zkoumaný signál. Možná se vám to zdá prapodivné, proč výkon souvisí s úrovní tímto způsobem, ale mimoděk tuto souvislost již léta využíváte:
Jde o známé triviální výpočty výkonu podle činitelů Ohmova zákona. Konstantou úměrnosti je zde odpor, případně pro střídavé harmonické signály impedance. Signál sám o sobě „nepracuje“ do žádné impedance, ale to neznamená, že nemůžeme porovnávat jejich energetické poměry. Pokud jde o signály z reálného světa, mimoděk se prostě předpokládá, že signály zkoumáme za stejných podmínek, jinak musíme zohlednit i podmínky. Mimochodem jedním z velice běžných případů, kdy signály nejsou za stejných podmínek, je udávaný parametr napěťový zisk zesilovače. Ten bývá mezi 20 a 30 dB, přestože poměr výkonů je klidně dalších 54 až 64 dB, pokud se zohlední impedance (10 kOhm vstupní a 4 Ohm zatěžovací). Jelikož za těchto podmí-nek je energie stejně velkého napěťového signálu před a za zesilovačem zcela jiná, osobně bych se využívání decibelů zde vyhnul, neboť decibel vyjadřuje skutečné výkonové poměry. Zde však „decibelový“ poměr před a za zesilovačem může být 0 dB, avšak skutečný poměr výkonů klidně 30 dB. Každý se s tímto faktem zkrátka musí naučit nějak žít, i když je to, věřte mi, těžké. (Ilustrace 4)
Nyní ale zpět k ETC – jakmile jsme převedli signál na jeho výkon, je třeba ještě provést převod do dB škály pomocí dekadického logaritmu (no jako vždycky). Díky tomu jsou v ETC vidět daleko lépe různé odrazy až o 20-30 dB pod úrovní maxima, což je někdy velice užitečné, neboť i ty dokážou hrát roli při vnímání zvuku, efektu hřebenového filtru atd. No a díky ETC zkrátka „vyplavou“. Pro pořádek ještě uvedu vzorec pro výpočet úrovně v dB v závislosti na poměru výkonů (P) a napětí (U):
Přechodová odezva
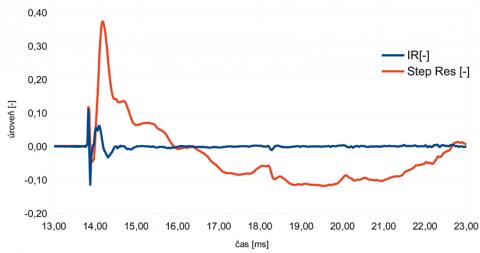
Ještě než se pustíme dále, zmíním pro pořádek ještě přechodovou odezvu, tedy odezvu na jednotkový skok. Tak, jak je impulzní odezva odezvou na maximálně krátký impulz, je přechodová odezva odezvou na maximálně strmou změnu úrovně. Jak spolu souvisí skok a impulz? Jednoduše – skok představuje integraci (resp. sumaci) impulzu, neboli sečtení jednotlivých bodů signálu (každý další bod je součtem všech předchozích). Před impulzem jsou všechny nulové, za impulzem také, takže jejich sumace bude až do impulzu nula, okamžikem impulzu se změní na jedna a tam už zůstane (přičítání vzorků s nulovou úrovní výsledek nezmění). Proto platí: Jednotkový skok je integrál diracova impulzu, takže přechodová odezva představuje integraci impulzní odezvy. Naopak diracův impulz je derivací jednotkového skoku atd. (Ilustrace 5)
Obě charakteristiky tedy v sobě nesou naprosto stejnou informaci a na pohled spolu souvisejí ještě více, než impulzní odezva a frekvenční charakteristika. Dle mého názoru tam tedy není vidět o mnoho více, než v impulzní odezvě, výjimkou mohou být snad dynamické projevy u výkonových zesilovačů, to jsou však jevy značně nelineární, tudíž mimo vytyčenou oblast tohoto článku.
Kde vzít impulzní odezvu bez šumu a nekrást?
Impulzní odezva má v akustice jeden zásadní problém – sama o sobě má poměrně malou energii a kromě toho je při reálném měření zatížena odrazy a hlukem/šumem, které leckdy takřka znemožňují správnou analýzu. Něco lze získat opakovaným měřením a průměrováním, čímž se do jisté míry potlačí vliv šumu, ale není to zrovna pohodlné. Je totiž potřeba si uvědomit, že celková energie impulzu se při výpočtu spektra rozkládá na jednotlivé složky, které v součtu pochopitelně musí mít shodnou energii/výkon. A když tedy máme spektrum běžně několika desítek tisíc vzorků, tak výkon každé spektrální složky je již tak dost malý, že impulz reálně docela rychle odeznívá. Nicméně matematici jsou lidé bystří a vymysleli řadu různých nástrojů, jak si poradit. Impulz, jakožto energetický signál (celková energie jednoho impulzu je omezena bez ohledu na dobu jeho měření) nahradili výkonovým signálem, které se lépe měří a nemají problém s dostatečným odstupem od šumu. Různých postupů a metod je jistě celá řada, ale pro ilustraci budeme příště – v druhém pokračování tohoto článku – pokračovat tou snad nejznámější...