FFT
Neboli Fast Fourier Transform je efektivní způsob výpočtu fourierovské transformace. Principiálně sahá její objevení až ke Karlu Fridrichu Gaussovi, avšak tehdy publikované principy nevešly ve všeobecnou známost. Po několika dalších znovuobjeveních nastal definitivní průlom až po publikování metod efektivního výpočtu s možností použití počítače, jehož autory byli pánové James Cooley a John Tukey v roce 1965. Principiálně vychází výpočet z diskrétní varianty fourierovské transformace (DFT), která je však náročná na počet kroků násobení (tzn. počítači dlouho trvá výpočet), které rostou s druhou mocninou počtu vzorků pro DFT. Pánové Tukey a Cooley proto přišli s myšlenkou rozdělení intervalu na několik menších (dva a více), a jejich zpracování metodou DFT „samostatně“. Ale konec dějepisu a vzhůru do praxe. FFT tedy rychle vypočítá komplexní spektrum signálu. Má však tu vlastnost, že na rozdíl od DFT ji lze v nejpoužívanější formě počítat jen z 2n vzorků. Dále platí, že spektrum má stejný počet vzorků (bodů), jako původní signál, které leží lineárně rozloženy v intervalu 0 – Fs (přesněji Fs - 1 bod), tedy od nuly (stejnosměrná složka) až po vzorkovací frekvenci, přičemž spektrum od Fs/2 do Fs je zrcadlovým obrazem spektra od 0 do Fs/2.
Z toho vyplývají VELICE DŮLEŽITÉ DŮSLEDKY:
1) Nejnižší frekvencí, kterou lze ve spektru zobrazit, tedy první bod spektra s nenulovou frekvencí, je rovna Fs/N, kde N je počet vzorků. Pro vzorkovací frekvenci 48 kHz a počet bodů 32768 je tak nejnižší nenulová frekvence 1,465 Hz.
2) Tato frekvence rovněž představuje rozlišení spektra, tedy frekvenční krok.
3) Vzorky spektra jsou lineárně rozloženy, při klasickém logaritmickém měřítku horizontální osy pak dojde k nerovnoměrnému rozložení bodů spektra – rozlišení například 10 Hz zabírá zcela jinou oblast kolem frekvencí 50 Hz, než v oblasti 50 kHz.
4) Jeden bod spektra nenese informaci o jediné přesné frekvenci, ale v podstatě reprezentuje energii celého frekvenčního pásma Fs/N signálu. To je podstatné v tom případě, kdy analyzovaný úsek neobsahuje celistvý počet period signálu, což je prakticky vždy. Skutečně obsažené frekvenční složky se pak přesně nekryjí s body spektra, takže při pohledu s dostatečným rozlišením a dynamickým rozsahem můžeme vidět různé projevy tohoto jevu (energie harmonické složky je rozložena mezi více bodů spektra, různé tvary přechodu mezi patou špičky a šumovým pozadím atd.)
Tyto vlastnosti tak základním způsobem omezují možnosti výpočtu spektra a podle požadavků na rozlišení musíme přizpůsobit délku vzorkovacího intervalu. Při měření v reálném čase zase naopak délka intervalu způsobuje snížení možností sledování dynamických změn – je rozdíl, zda máme za 1s deset spekter s horším rozlišením, nebo jedno spektrum s vysokým rozlišením. Při výpočtu tzv. 3D spektra, tedy náhledů signálu zvaným Spectral View, Spectrogram (při měření reprosoustav i Waterfall) atd., tak leží požadavky na časové a frekvenční rozlišení přímo proti sobě a je potřeba najít vhodný kompromis podle aktuálních potřeb.
Ono nejde jen o nějakou matematickou konstrukci, ale takřka hmatatelnou realitu. Když totiž máme v signálu dvě frekvence vzdálené o 1 Hz, bude výsledným produktem těchto složek sinus o „frekvenci“ aritmetického průměru obou složek, který bude amplitudově modulovaný s periodou 1 Hz. Abychom však mohli ve spektru rozdělit od sebe obě frekvence, musíme mít ve zkoumaném úseku v praxi dvě periody této „amplitudové modulace“, tedy 2 sekundy signálu a rozlišení spektra 0,5 Hz, jinak ani na pohled úsek signálu nerozlišíme od sinu (při úseku třeba jen 10 ms a frekvencích 1000 a 1001 Hz). Jedině tak se totiž ve spektru obě složky ukážou samostatně, mezi nimi přitom bude propad, který obě složky jasně oddělí.
Okna
Nyní byste již měli vědět, jakým způsobem souvisí délka úseku signálu pro FFT s rozlišením vypočteného spektra. Rovněž jsme zevrubně nastínili možné problémy s přítomností odrazů v impulzní odezvě systému zejména při akustických měřeních. Ty totiž způsobují efekt podobný hřebenovému filtru ve výsledném spektru – když se totiž impulz ve vyhodnocovaném úseku opakuje, způsobí, že některé spektrální složky zdůrazní, zatímco jiné potlačí. Princip je snadno představitelný – máme relativně idealizovaný tvar impulzní odezvy. Její spektrum se počítá podobně, jako korelace jednotlivých spektrálních složek s touto odezvou, tj. součin dané složky (jednotkový sinus o dané frekvenci, pravda v komplexním oboru kvůli fázi, ale to teď nechme) s touto odezvou. Těchto složek je tolik, kolik je bodů spektra.
Nyní si představíme další posunutý impulz s o něco nižší úrovní. Když se jeho poloha a polarita (přesněji jeho funkční hodnoty) budou více méně krýt s průběhem dané spektrální složky (jedno o kolik period vzdálené od počátku), bude korelace této složky s analyzovaným signálem vyšší, než u jiné složky, kde impulz padne do míst, kde funkční hodnoty dané složky mají opačnou polaritu vzhledem k impulzu a tedy výsledná korelace bude nižší.
Odrazy v akustických měřeních tak způsobují vážné problémy. Dříve při analogových měřeních byla prakticky jedinou možností bezdozvuková komora, nicméně dnes díky digitálním systémům a matematickým nástrojům máme poměrně bohaté možnosti, jak se odrazům téměř zadarmo vyhnout: okénkové funkce (windowing).
Okénkové funkce jako takové představují takřka jeden matematický obor. Mají zásadní vliv na tvar výsledného spektra, zejména na selektivitu a efekt „maskování“ (viditelnost spektrálních složek s nízkou úrovní poblíž významné spektrální špičky, de facto tvar paty spektrální složky). Pro nás ale má zásadní význam časové omezení signálu, které má nižší vliv na selektivitu, než omezení délky úseku FFT .
Jak jsme si řekli, délka FFT určuje počet bodů výsledného spektra. Budeme (například analyzovat úsek sinusového signálu o velké amplitudě, například z důvodu měření harmonického zkreslení), vezmeme-li vzorek tak jak je, nebude spektrum vypadat příliš hezky, zejména proto, že reálný úsek signálu obsahuje složky, které se do analyzovaného úseku signálu nevejdou celistvým počtem period.
Spektrální špička se bude ve spektru s klesající úrovní pozvolna rozšiřovat a viditelný dynamický rozsah nebude příliš velký. Je to tím, že jsme signál pro FFT ostře vyřízli (pravděpodobně nezačínal v nule, ani v ní nekončil) a jeho složky nebudou přesně souhlasit s body spektra FFT. Použili jsme totiž tzv. obdélníkové okno (rectangular window). Díky těmto nespojitostem a nepřesnostem ve vzorkovaném signálu tak bude vyšší vzájemná energie složek, které by jinak ve spektru neměly být, a proto se ve spektru projeví (zvýšením šumového pozadí, stejně jako výkyvy v případném tvaru spektra).
Spektrum signálu totiž bude daleko lépe vypadat, pokud analyzovaný signál před výpočtem spektra upravíme tak, aby se na začátku i na konci blížil nule, tedy jakýsi fade in a fade out. To je právě účelem okénkové funkce – oříznout signál před výpočtem FFT tak, aby výsledné spektrum mělo pro dané účely co „nejpoužitelnější tvar“.
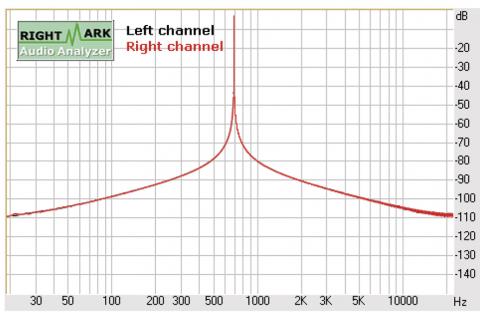
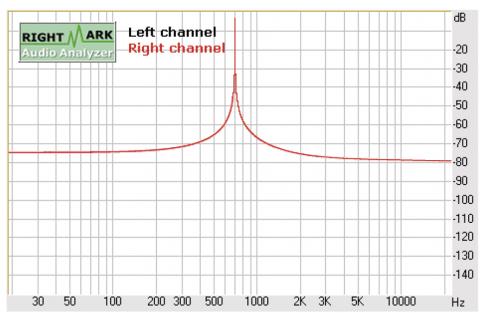
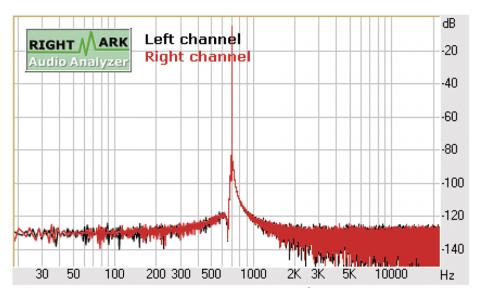
Různé tvary křivky „ztlumování“ mají tvar na charakter zobrazení (omezení vzájemné korelace mezi nejen blízkými body spektra, schopnost vydělit složku ze šumu atd.), ale nebudeme se jimi hlouběji zabývat,vyčerpávající popis v angličtině lze nalézt na wikipedii (http://en.wikipedia.org/wiki/Window_function). Nás bude zajímat jiná vlastnost okna – schopnost oříznout impulzní charakteristiku tak, abychom eliminovali odrazy. Vhodnou kombinací délky FFT a délky okna lze leckdy dosáhnout uspokojivých výsledků pří měření aparátu, i pokud nemáme bezdozvukovou komoru. Nicméně pro ilustraci jevu přikládám čtyři obrázky dvou podobných signálů – sinus 689,0625 Hz (perioda 64 vzorků) a sinus 700 Hz (nesoudělná frekvence jak s délkou FFT, tak vzorkovací frekvencí), délka signálu vždy 32768 vzorků, vzorkování 44100 kHz /16 bitů, FFT pomocí programu RMAA 5.5. (Ilustrace 16 - 19)
Omezení úrovně při použití oken
Tím se dostáváme střemhlav k nejdůležitějšímu způsobu eliminace odrazů při měření – omezení okna při měření spektrální charakteristiky. Jedinou cenou za eliminaci odrazů je de facto jen omezení dolního mezního kmitočtu měření – frekvence, jejichž perioda je delší, než polovina délky okna, mají v důsledku „ořezání“ oknem omezenou úroveň oproti reálu. Jinými slovy, výsledné spektrum vypadá, jako by od určité frekvence dolů bylo upraveno HP filtrem. Na tento jev je potřeba dávat si pozor, protože pokles samozřejmě neodpovídá realitě.
Frekvencím pod 2/Tokna zkrátka není možné věřit. Dalším důsledkem, který ale není obvykle zrovna na závadu, je zhoršení selektivity analýzy. Není to však obvykle na závadu, protože se ve výsledku měřená charakteristika spíše „vyčistí“ (eliminací odrazů a nižší selektivitou), přičemž nedojde k takové ztrátě informace, jako při rozmazání například 1/3okt filtrem. Pokud volbou délky okna odstraníme všechny odrazy, bude takové měření v podstatě ekvivalentní měření v bezodrazové komoře, a to jen za cenu horší selektivity a omezení platnosti měření na nízkých kmitočtech. Tam se ale stejně výrazně podepisuje prostor, takže samotná charakteristika reprosoustavy ovlivňuje výsledek jen z části. (Ilustrace 20 - 21)
Klouzavá okna
Pravým zázrakem se však okna stávají ve chvíli, kdy se jejich možnosti využijí do konce – proměnnou délkou okna (například okno Time Frequency Constant v programu Easera SysTune).
V praxi se totiž odrazy, a to i ty méně viditelné, podílejí na tom, že u vyšších frekvencí je charakteristika velice „chlupatá“. Abychom tyto odrazy eliminovali, museli bychom mít velice krátké okno (do 5 ms). To by však až příliš omezilo měření spodního pásma. Ovšem nikde není řečeno, že musí v průběhu výpočtu celého spektra FFT být totéž okno. Proto pokročilé programy nabízejí možnost použití okna s proměnnou délkou, takže pro každou frekvencí je použito okno jen s nezbytně nutnou délkou (například čtyři periody každé frekvence) a tak jsou odrazy takřka eliminovány, tedy s výjimkou případu, kdy je vzdálenost mezi odrazy srovnatelná s vlnovou délkou analyzované frekvence. Pak už se toho nedá moc dělat, snad hledat jiné místo k měření nebo měřit v různých vzdálenostech a výsledky zprůměrovat.
A sfázování systému? Na to si počkejte někdy příště. :-)