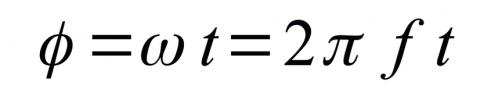MLS
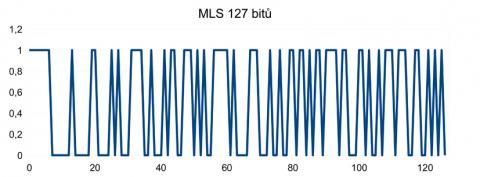
MLS znamená Maximal length sequence, tedy sekvence maximální délky. Jde o binární posloupnosti (signály) vhodných vlastností, které se hodí pro naše účely, a pochopitelně i pro řadu jiných. Délka takové sekvence je 2n-1 „bitů“, nelze tedy vytvořit MLS signál libovolné délky. MLS signál je takzvaný pseudonáhodný signál, tedy jeho statistické vlastnosti jsou velice podobné šumu (prototyp pseudonáhodného signálu). První vlastností je zcela ploché spektrum (ale jen za jedné přesně dané podmínky, viz dále) a druhou je, že jeho autokorelační funkce (korelace signálu se sebou samým) se velice podobá diracovu impulzu. Jinými slovy, při výpočtu korelace MLS signálu se sebou samým (autokorelační funkce) vyjde maximální korelace pro nulové vzájemné posunutí a teoreticky nulová korelace ve všech ostatních bodech/posunutích autokorelační funkce.
Tedy stejně jako u šumu. To nejpodstatnější však je, že když provedeme korelaci MLS signálu před a po průchodu zkoumaným systémem, získaná korelační funkce bude odpovídat impulzní odezvě zkoumaného systému. (Ilustrace 6)
Vzhledem k tomu, že při korelaci se de facto počítá (= integruje) celý úsek signálu, nejsou takové problémy s odstupem od šumu. Nemusíme navíc systém vybuzovat na vysoké úrovně, kdy se začínají na reálném zařízení ve větší míře projevovat nelinearity, které znehodnotí výsledek – všechny operace a předpoklady totiž stojí na tom, že systém je lineární, tedy alespoň dostatečně lineární pro naše potřeby, tzn. jeho nelinearity řekněme nemají významnou energetickou úroveň, aby se projevily na frekvenční charakteristice. Při přímém měření impulzní odezvy jsme totiž z důvodu maximálního odstupu byli nuceni systém vybuzovat na nejvyšší přijatelnou úroveň, což nepřímá metoda pomocí MLS elegantně obešla.
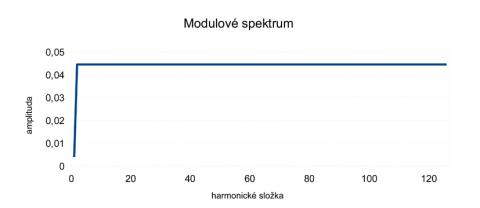
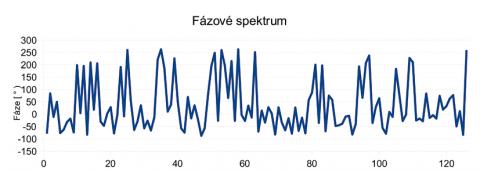
Poslední významnou vlastností MLS je ono zmíněné ploché spektrum, obdobné spektru bílého šumu. To je skutečně pravda, ale platí to v případě, kdy vzorkovací frekvence AD převodníku odpovídá bitové frekvenci MLS signálu a délka úseku signálu pro výpočet FFT je takřka shodná s délkou sekvence MLS. Kdybychom vzorkovali vyšší frekvencí, bude se více a více projevovat skutečné spektrum, které připomíná graf |(sin (x)) / x| s přihlédnutím k zrcadlení spektra od vzorkovací frekvence. Kdyby délka úseku pro FFT byla několikanásobně delší, než MLS (obsahovala by tedy několik period MLS), bylo by spektrum nespojité (proloženo nulami), neboť některé frekvence, jejichž celistvý počet period by se nevešel do jednoho úseku MLS, by v signálu nebyly obsaženy. Vidíme tedy, že obecně udávaná vlastnost MLS – ploché spektrum podobné bílému šumu, platí jen za určitých situací a nelze ji tedy považovat za obecnou. Podobné je to s předpokladem, že FIR filtry mají lineární fázi (platí jen za předpokladu, že FIR filtr má symetrickou impulzní odezvu – špička se nachází v polovině délky impulzní odezvy). Jen pro úplnost ještě dodám, že jak uměle generovaný bílý šum, tak MLS mají časový průběh pseudonáhodný, avšak amplitudovou charakteristiku (amplitudové spektrum) mají zcela plochou. Takto vyrovnané spektrum však nepředstavuje nic náhodného ani pseudonáhodného. Ona náhodnost se totiž skrývá ve fázové charakteristice (viz dále), která již vypadá docela „náhodně“. (Ilustrace 7 - 9)
Přesto, že je metoda MLS velice užitečná a odstraňuje řadu problémů přímého měření impulzní odezvy, sama o sobě nedokáže eliminovat vliv odrazů, její smysl je prostě někde jinde. Na eliminaci odrazů však máme další nástroje, které lze s MLS účinně kombinovat.
Co je to vlastně fázová charakteristika?
Nyní se dostáváme do šedých oblastí, opředených rouškou tajemna, které oddělují mágy od laiků. Fázová charakteristika a fáze obecně je totiž trochu zamotaná (aby ne, když se stále točí) a chce to trochu toho duševního úsilí, aby se v ní člověk zorientoval. No a kdo je od přírody líný používat mozek, tomu zbudou jen výmluvy na praxi a její vzdálenost k teorii (jež však sám není schopen obsáhnout, tak v praxi tápe a používá tak „osvědčená nastavení“).
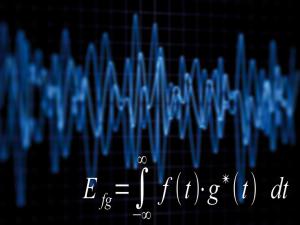
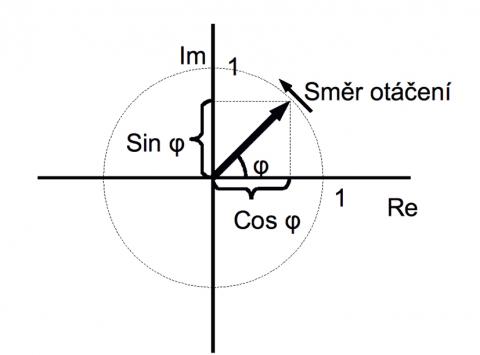
Co je to fáze? Jde o matematický nástroj, který je velmi užitečný při práci s harmonickými signály (= sinus/cosinus). Jen připomenu, co vlastně znamená sinus:
Bude-li bod S obíhat po jednotkové kružnici konstantní rychlosti, například 1x za sekundu, s výchozí polohou pro čas t=0 v bodě [1;0], bude průmět okamžité polohy bodu S do osy Y odpovídat funkci sin(360°. f.t) (f je frekvence, t je čas). Fází v tomto případě rozumíme argument funkce sinus, tedy v jaké fázi oběhu po kružnici se bod S nachází. Všimněte si prosím toho, že v tomto případě znamená obrácení fáze de facto změnu směru toku času (otočení směru oběhu bodu S), žádné obrácení polarity. Sice platí, že sin(-x) = -sin(x), ale již pro cos (x) to neplatí. U obecného signálu, složeného z jednotlivých harmonických složek, pak změna polarity a toku času je něco zcela jiného. Zkrátka tak, jak se zvuk liší od sinus, tak se liší i důsledky aplikace operací na sinus a zvukový signál, a vždy je třeba mít na paměti, co děláme! Jak je uvedeno výše, fáze je dána vztahem:
A právě to f je smrtelně důležité. Při přepočtu na stupně pouze nahradíme výraz 2π za 360°, což je mezi zvukaři častější. Fázová charakteristika, jakožto součást frekvenční charakteristiky, totiž udává, s jakým fázovým posunem se ocitnou jednotlivé spektrální složky na výstupu systému vůči situaci na vstupu. Pro časový tvar signálu je přitom sfázování všech složek zásadně důležité – budou-li jednotlivé složky jinak vzájemně posunuté, změní to zásadním způsobem tvar signálu, jeho maximální úrovně...prostě všechno. Přitom takový signál bude mít při pohledu na spektrum (správně modulovou charakteristiku) zcela stejné vlastnosti. Kamenem úrazu však je, že v reálném světě je dochází mezi vstupem a výstupem jednak k prostému časovému posuvu (všechny složky o stejný čas, nemění tvar signálu, fáze složek narůstá s frekvencí), druhak k fázovému zkreslení (mění tvar signálu). Výsledná fázová charakteristika je pak kombinací obou složek a pro správnou analýzu je třeba je od sebe oddělit.
|
Komplexní čísla jsou matematickým nástrojem, který přidává normálnímu (reálnému) číslu ještě další složku neboli rozměr. Rozměrem této složky je tzv. imaginární číslo i (v elektrotechnice a fyzice značené j, neboť i bylo rezervováno pro proud), jež má tuto vlastnost j2 = -1. Z hlediska signálů umožnilo použití komplexních čísel snadné počítání s fázory, neboť informace o modulu i fázi jsou obsažené v každém komplexním číslu. Rovněž se odstranily některé potíže v okamžicích průchodu signálu nulou, kdy například při dělení nebo násobení takovou funkcí v komplexní rovině již nedělíme/nenásobíme nulou, ale funkcí, která má nenulový modul a určitou fázi. |
Situaci komplikuje fakt, že například konstantní fázové zkreslení +90° (ideální derivační článek) dává sice plochou fázovou charakteristiku, ale zásadním způsobem mění tvar signálu – jde totiž v základu o HP filtr 6dB/okt. Přitom konstantní časové zpoždění 1 ms znamená posun fáze 36° na 100 Hz, 360° (1 periodu) na 1 kHz a 3600°na 10 kHz (10 period). Pro správné zobrazení fázové charakteristiky a oddělení prostého zpoždění od fázového zkreslení, je tedy nutné správně kompenzovat časový posuv, tedy odečítat tak dlouho konstantní čas, až bude časové zpoždění eliminováno.
V praxi při měření PA se toho snažíme dosáhnout pomocí úpravy parametru delay offset nebo podobným. Vtip je v tom, že nikdy přesně nevíme, kdy jsme právě odečetli celé časové zpoždění a vidíme jen fázové zkreslení, už proto, že jedno je součástí druhého, přesně tak jdou určit jen relativní rozdíly. Vzhledem k praktickým potřebám je však dostačující upravit delay offset tak, aby v momentálně sledovaném pásmu byl graf čitelný a relativně plochý. Pomoci může změna vertikálního rozlišení například na +/- 360° i více. Při fázování systému pak tento offset NESMÍME MĚNIT, pokud k tomu nemáme oprávněný důvod. Zdá se vám to komplikované? Je to ještě o něco horší – dodnes nevím o tom, že by se vědci jednoznačně shodli na tom, jak moc je slyšet případné fázové zkreslení, nebo přesněji fázová nelinearita, ani to, jaké jsou meze tohoto zkreslení, které je možné považovat za „bezpečné“.
Modul, fáze, amplituda
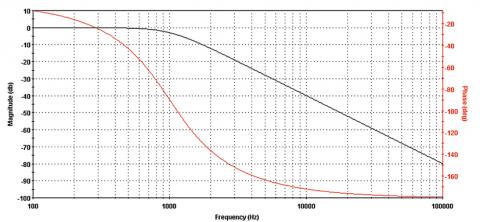
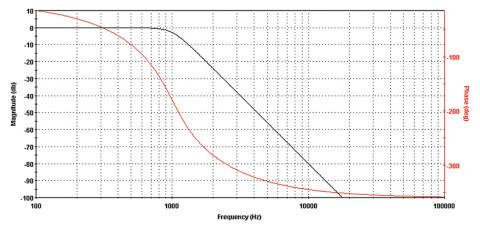
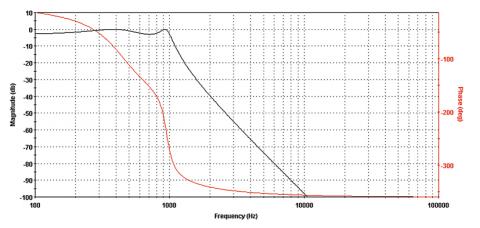
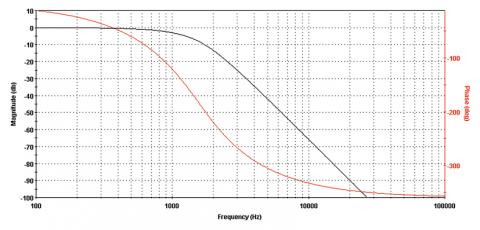
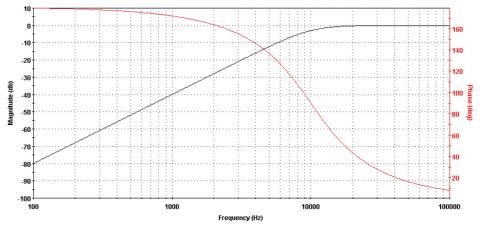
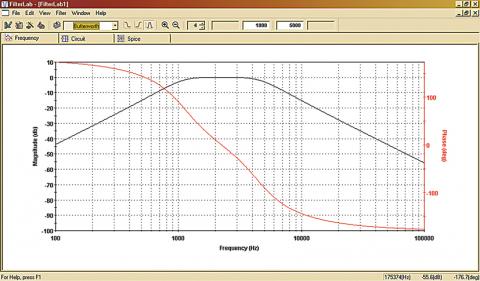
Čímž se dostáváme k další důležité terminologii, popisující parametry fázorového modelu. Jak jsme si řekli, harmonický pohyb modelujeme v XY souřadnicích pohybem bodu po kružnici, tedy rozkládáme jej do dvou os, reálné a imaginární složky. Takový pohyb ovšem lze znázornit i v tzv. polárních souřadnicích, které charakterizuje velikost (vzdálenost od počátku) a úhel, což odpovídá fázi. V obou souřadnicových systémech však mluvíme v souvislosti o harmonických dějích o tzv. fázorech, což je obdoba vektoru, a je popsána právě velikostí (tzv. modulem) a fází. Při zobrazení harmonického signálu v časové rovině pak hovoříme o amplitudě, což je bod maximální výchylky/úrovně, která odpovídá modulu fázoru a nastává v okamžiku, kdy je fázor v ose s reálnou osou a imaginární složka je tedy v daném okamžiku nulová. Pro zajímavost nyní uvedu simulované frekvenční amplitudové a fázové charakteristiky několika běžných filtrů typu horní propust, dolní propust a pásmová propust. Použit byl volně dostupný program FilterLab od Microchip Technology, Inc. (Ilustrace 10 - 15)
(Pokračování příště...)